MESURE - Mesures thermiques

MESURE - Mesures thermiques

Les mesures thermiques sont nées du besoin de traduire par des repères numériques les sensations de chaud et de froid liées à la température. Celle-ci est donc directement accessible à nos sens, mais d’autres grandeurs thermiques moins évidentes ont été précisées par la suite, telles que les quantités et les flux de chaleur, dont la mesure s’est révélée d’une importance considérable dans toutes les branches de la science.

La détermination des températures demeure cependant la base de toutes les mesures thermiques. Tandis que la thermodynamique donnait de cette grandeur physique une définition précise, le domaine des températures mesurables débordait largement celui des sensations perceptibles par le corps humain (du millième de degré absolu, à plusieurs millions de degrés dans les plasmas thermonucléaires).

La notion de température n’a de sens que pour un très grand nombre de particules (atomes, ions, molécules, électrons, photons, etc.) en interaction. Chacun des mouvements (rotation, vibration, translation) des particules possède un certain nombre de degrés de liberté. Prise séparément, chaque particule peut avoir des quantités de mouvement de grandeur ou de direction quelconques; si bien que, en ce sens, l’agitation thermique apparaît désordonnée. Toutefois les échanges dus aux chocs incessants entre particules tendent à réaliser entre celles-ci une répartition parfaitement définie de leurs énergies cinétiques: lorsque cette répartition est réalisée, l’ensemble des particules est en équilibre thermodynamique. On peut alors exprimer le nombre relatif N de particules dont les énergies se situent dans un intervalle compris entre E et E + E: ce nombre dépend du niveau d’énergie E, et d’un paramètre qui est précisément la température. Ce calcul de répartition fait l’objet d’un chapitre de la thermodynamique statistique.

Il arrive qu’en présence d’une excitation quelconque (réaction chimique, onde de choc, champ électrique agissant sur des électrons libres, etc.) on obtienne des répartitions d’équilibre des énergies cinétiques qui correspondent à des températures différentes, soit pour différentes catégories de particules qui coexistent dans un système matériel, soit pour plusieurs types de mouvements dont peuvent être animées des particules de même nature. C’est ainsi qu’un ensemble de molécules peut avoir, dans de telles conditions, une température de translation, une température de rotation et une température de vibration distinctes, si elles possèdent les degrés de liberté correspondants. Ou bien encore, dans un plasma composé d’ions positifs, d’électrons libres et de particules neutres, il peut y avoir des températures propres à chacun des constituants. Si l’on supprime l’excitation responsable de ces différences, toutes les températures tendent à s’égaliser, de manière à réaliser l’équilibre thermodynamique.

La «température» de la lumière mérite un examen particulier pour le rôle considérable qu’elle joue dans les mesures thermiques. Comme toute forme de matière, le rayonnement électromagnétique d’origine thermique équilibre sa température avec celle du milieu dans un système fermé (corps noir). La loi de distribution de l’énergie des photons correspond seulement à une répartition des fréquences (et non des vitesses); son calcul aboutit à la loi classique du rayonnement d’un corps noir (formule de Planck, cf. THERMIQUE).

1. Quantités de chaleur et propriétés thermiques des corps

On a remarqué de tout temps que, si l’on mettait en contact un corps chaud et un corps froid, le corps chaud se refroidissait alors que la température du corps froid s’élevait. Généralisant ce principe, l’hypothèse de Fourier consiste à admettre que, dans un milieu où règne un gradient thermique, de la chaleur s’écoule en raison de ce gradient. La quantité de chaleur qui traverse l’unité de surface pendant l’unité de temps (densité du flux thermique) est représentée par le vecteur:

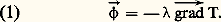Dans cette expression, T est la température locale et un coefficient, appelé conductibilité thermique, qui dépend de la nature du matériau conducteur et de T. Si l’on pose:

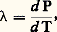P apparaît comme le potentiel dont dérive み (soit み = 漣 gradP). Si un flux de chaleur traverse la surface qui entoure un élément matériel non compressible de volume 嗀益 et de masse volumique 福, ce volume subit une élévation de température d T, à condition de ne pas être le siège d’un changement d’état physique qui absorbe la chaleur (fusion, par exemple). Si l’échauffement s’effectue sous pression constante, cas le plus général, on représente la quantité de chaleur accumulée dans le volume 嗀益 par:

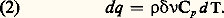Dans cette expression, C^p est un coefficient qui, comme, dépend de la nature du corps et de sa température: c’est la capacité thermique massique à pression constante.

En écrivant la loi de conservation de la chaleur (dans le volume 嗀益, la différence entre la quantité de chaleur qui entre et celle qui sort est égale à la quantité de chaleur accumulée), on déduit des relations (1) et (2) l’équation fondamentale de la thermocinétique:

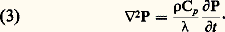La forme de cette relation montre que, dans un milieu conducteur de la chaleur, le potentiel thermique obéit à une loi dite de diffusion, dont le coefficient/ 福 C^p est appelé «diffusivité thermique».

Dans un milieu compressible (gaz), où une équation d’état relie la température, la pression et la masse volumique, on ne peut élever la température sans modifier au moins l’une des deux autres variables. Dans l’expression de dq , le terme correspondant à l’élévation de température d T, à masse volumique constante, introduit un coefficient analogue à C^p dans l’équation (2): c’est la capacité thermique massique à volume constant Cv. Le rapport:

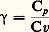définit une propriété thermique fondamentale des gaz, qui intervient dans tous les calculs où la compressibilité entre en jeu.

Un autre coefficient important, dont la détermination fait partie des mesures thermiques, est mis en évidence par la résolution de l’équation (3), dans le cas d’une diffusion unidirectionnelle à partir de la surface d’un milieu semi-illimité. Si l’on maintient une élévation de température constante à la surface d’un tel milieu, en lui faisant toucher un corps chaud, la quantité de chaleur retirée à ce corps chaud par unité de surface s’exprime par:

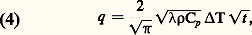où le temps t est compté à partir de la mise en contact. Le coefficient 福 C^p , propre au milieu qui absorbe la chaleur, est appelé effusivité (face=F0019 連福C^p est le coefficient d’arrachement thermique).

Le domaine des mesures thermiques proprement dites se limite aux grandeurs et aux coefficients qu’on vient de définir.

2. Unités de mesure et constantes thermiques fondamentales

L’unité légale française de température (kelvin) est complètement définie en attribuant au point triple de l’eau une température absolue de 273,16 K. Dans l’échelle Celsius (dont le degré est égal au kelvin K), on note zéro la température du mélange eau-glace sous pression normale (1,013 bars). Les pays de langue anglaise utilisent pour définir la température absolue le degré Rankine égal à 5/9 K; dans l’échelle Fahrenheit, dont le degré est égal au degré Rankine, le mélange eau-glace correspond à une température de 32 degrés. Signalons qu’on emploie couramment, en physique des plasmas et en physique nucléaire, l’électronvolt pour exprimer une température, alors qu’il s’agit d’une unité d’énergie (en dehors, d’ailleurs, du système métrique).

Les quantités de chaleur s’expriment par les mêmes unités que l’énergie, et les flux thermiques sont homogènes à des puissances. Les principales unités thermiques sont réunies dans le tableau 1, où l’on a porté pour mémoire des unités non métriques telles que la calorie, dont l’usage devrait être abandonné en faveur des unités décimales. Le tableau 2 rassemble les principales constantes physiques qui interviennent dans les mesures thermiques.

3. Mesure des températures

La thermométrie (ou pyrométrie, s’il s’agit de températures élevées) fait appel à des méthodes extrêmement nombreuses; on se bornera à en exposer les principes dans leurs grandes lignes.

Les points fixes et les étalons de base

L’étalonnage des thermomètres est effectué à partir de phénomènes physiques dont la température est parfaitement reproductible: ce sont les points fixes. En dehors du point triple de l’eau utilisé pour définir le degré, les points fixes jouent le rôle d’étalons secondaires.

La Conférence internationale réunie en 1968 a adopté un certain nombre de points fixes (tabl. 3) dont certains sont connus au dix-millième de degré près; leurs valeurs résultent de mesures très précises, mais il convient de signaler que celles-ci pourront évoluer en fonction des progrès de la métrologie thermique. De plus, des thermomètres étalons ont été normalisés pour indiquer les divers intervalles de température.

Principales méthodes de mesure des températures

Les méthodes thermométriques peuvent se présenter sous deux aspects; ou bien elles permettent la mesure directe de la température dans le milieu même où l’on veut la déterminer, ou bien elles s’appliquent à la température d’un capteur que l’on plonge au sein de ce milieu; le capteur doit alors prendre une température identique à celle du milieu, ou éventuellement une température qui lui soit reliée par une fonction connue.

Méthodes cinétiques

Elles consistent à déterminer directement la température d’un gaz à partir des vitesses d’agitation thermique. C’est ainsi que, dans les plasmas très chauds (au-dessus de 5 憐 10⁴ K), les raies d’émission de certains atomes ou ions (tels que H, O, He, Ar, etc.) se trouvent décalées par effet Doppler en raison de l’agitation thermique; comme les vitesses ont des directions quelconques, les raies apparaissent élargies. La mesure spectrométrique de la largeur de raie (entre les deux points correspondant au demimaximum) permet de calculer la température ionique, avec une précision de l’ordre de 10 p. 100, par la formule:

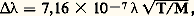où et sont exprimés en angströms et T en kelvins, M étant la masse molaire.

La température des électrons d’un plasma peut être mesurée à partir de la caractéristique tension-courant d’une sonde (sonde de Langmuir ), comportant des électrodes introduites dans le plasma, et que l’on peut porter à des potentiels négatifs réglables. Le nombre des électrons du plasma capables d’atteindre une telle sonde répulsive, et par suite l’intensité du courant collecté, dépend de la répartition des vitesses de ces électrons, donc de la température électronique (plus précisément du rapport e V/k T, si e est la charge de l’électron et V la différence de potentiel entre sonde et plasma). Cette méthode est d’un usage courant en physique des plasmas.

Les méthodes qui viennent d’être citées trouvent des applications dans les sciences aérospatiales (plasmas d’échauffement cinétique en vol ou en soufflerie), et dans les sciences nucléaires. Signalons aussi que la mesure de la température électronique de l’ionosphère est faite avec une bonne précision (à quelques centièmes), grâce à l’élargissement par effet Doppler d’une onde électromagnétique émise du sol et diffusée par le milieu: chaque électron libre, excité par l’onde, émet un rayonnement dont la fréquence est celle de l’onde incidente, décalée par effet Doppler dû à la vitesse propre de l’électron (sondeur à diffusion).

Méthodes liées à l’équation d’état d’un gaz ou d’un plasma

La pression d’un gaz proche de l’état parfait et chauffé à volume constant s’élève de façon sensiblement proportionnelle à sa température: c’est le principe du thermomètre à hydrogène (ou à hélium), constitué d’un réservoir de gaz relié à un dispositif manométrique. La précision de cette sonde thermométrique est très grande et on l’a longtemps utilisée comme étalon de laboratoire.

Un procédé, qui a donné lieu à de nombreuses applications, consiste à déduire la température d’un gaz d’une mesure de sa masse volumique, sa pression étant connue. Pour les gaz denses, on peut utiliser l’indice de réfraction n , lié à la masse volumique par une loi de la forme: (n 漣 1)/ 福 = C ^te , ou bien l’absorption d’un faisceau 廓 délivré par une source radioactive (jusqu’à quelques 10³ K). Dans un gaz raréfié (10^-4 à 10^-10 g/cm³), on peut déterminer la masse volumique locale à partir de l’intensité de la luminescence excitée par un faisceau électronique qui traverse le gaz (cette méthode qui a l’avantage d’être ponctuelle, puisqu’on peut mesurer l’émission lumineuse en chaque point du trajet du faisceau, est mise en œuvre dans des souffleries de l’O.N.E.R.A.).

Les thermomètres acoustiques mesurent, au sein d’un gaz, la célérité d’un ultrason, émis, par exemple, à l’aide d’un cristal piézo-électrique: cette célérité est proportionnelle à: face=F0019 連 塚RT/M, si 塚 désigne le rapport des chaleurs massiques du gaz et M sa masse molaire, grandeurs supposées connues. Cette méthode, assez peu précise, peut être utilisée jusqu’à 10⁴ K.

Les pyromètres à écoulement (ou pneumatiques), utilisables pour les gaz jusqu’à quelques 10³ K, ne sont pas encore couramment répandus dans l’industrie ou dans les laboratoires; ils présentent toutefois beaucoup d’intérêt malgré leur précision assez faible, grâce à leur robustesse et à leur simplicité. Ils se composent d’une conduite dans laquelle le gaz est aspiré; à chaque extrémité est disposé un déprimogène (tel que diaphragme, tuyère, etc.), comme le montre la figure 1; au niveau du déprimogène d’entrée, le gaz se trouve à la température ¹ que l’on désire mesurer, tandis qu’un système de refroidissement porte le gaz à une température connue ² (c’est par exemple, la température ambiante) au passage de l’étranglement situé à la sortie de l’appareil. Les pressions mesurées à l’amont et à l’aval de chaque déprimogène sont reliées par les équations de l’écoulement au rapport des températures ¹². La réalisation de vitesses soniques dans deux tuyères permet de ramener à deux seulement le nombre des mesures de pression; si p ¹ et p ² désignent celles-ci respectivement au niveau des deux tuyères, de sections S¹ et S², on a:

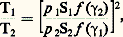avec:

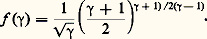Dans un plasma en équilibre thermodynamique, le taux d’ionisation thermique est défini par la formule de Saha qui traduit une équation d’état:

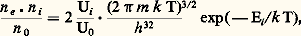où n ^e , n ⁱ et n ⁰ sont respectivement les densités des électrons, des ions et des particules neutres, Uⁱ et U⁰ les sommes d’état des ions et des particules neutres, m la masse d’un électron et Eⁱ l’énergie d’ionisation (k et h sont des constantes fondamentales, cf. tabl. 2). Toute mesure du taux d’ionisation permet alors de connaître la température; citons en particulier une méthode fréquemment utilisée: l’effet Stark , produit par le champ électrique interionique; il se traduit par un élargissement de raies d’émission (on utilise la série de Balmer de l’hydrogène, quand on peut introduire ce gaz en faible proportion dans le plasma); la détermination de température par ce procédé est assez précise jusqu’à quelques dizaines de milliers de degrés (on a, par exemple, pour la raie H 廓 une largeur de 5 nanomètres dans un plasma à 40 000 K, contenant 10¹⁷ électrons libres par centimètre cube). Pour l’élargissement des raies, l’effet Stark est largement prépondérant sur l’effet Doppler dans le cas des plasmas très denses.

Méthodes fondées sur la dilatation

Les thermomètres à dilatation de liquide sont des sondes qui comportent un réservoir de verre contenant le liquide et une tige graduée. Le mercure permet de mesurer des températures atteignant 350 ⁰C (et même 500 ⁰C, grâce à la surpression d’un gaz au-dessus de la colonne). Avec d’autres liquides (alcool éthylique, toluène, pentane), on peut effectuer des mesures à basse température (avec certains, depuis la température ambiante jusqu’à 漣 200 ⁰C). Une mesure n’est correcte que si toute la colonne de liquide est plongée dans le milieu dont on veut déterminer la température; sinon, on doit effectuer une correction, dite de colonne émergente.

La précision des thermomètres à mercure atteint facilement le dixième de degré; ils se prêtent à la réalisation de régulateurs très précis (avec contacts électriques) utilisés pour des thermostats.

La dilatation d’un fil métallique réfractaire est à la base du pyromètre Chevenard , qui équipe en particulier les systèmes de régulation des fours électriques (jusque vers 1 300 ⁰C). Un principe voisin est appliqué dans les bilames, constituées de deux lames métalliques à coefficients de dilatation différents et soudées l’une sur l’autre; un échauffement provoque une déformation que l’on mesure.

Méthodes fondées sur les changements d’état ou les forces de cohésion

Le thermomètre à tension de vapeur mesure la pression de la vapeur saturante au-dessus d’un liquide, cette pression dépendant de la température. On utilise, en particulier, un tel appareil en cryophysique avec l’hydrogène ou l’hélium liquides (cf. CRYOLOGIE - Cryophysique).

Les fusibles constituent des capteurs thermométriques à indications discontinues pour usage industriel: on peut répandre sur des surfaces solides des poudres fondant à des températures déterminées.

Les cônes pyroscopiques (cônes de Seger ) placés sur des surfaces solides se ramollissent et s’affaissent à des températures repérées (jusque vers 2 000 ⁰C): ils servent à évaluer grossièrement la température de pièces cuites dans des fours.

La viscosité d’un fluide est fonction de sa température; le pyromètre Job (ancien appareil de laboratoire) est constitué par une conduite où l’on maintient un débit gazeux constant; on mesure la chute de pression nécessaire pour assurer ce débit, celle-ci étant liée à la viscosité du gaz.

Méthodes fondées sur des variations de couleurs

Certaines substances changent de couleur à des températures déterminées; on les présente généralement sous forme de crayons avec lesquels on enduit des surfaces solides, ce qui permet d’évaluer approximativement des températures jusque vers 200 ⁰C.

Les métallurgistes savent aussi apprécier de façon grossière la température à laquelle on a chauffé des aciers, grâce à la teinte que le métal a pris de manière irréversible.

Méthodes thermoélectriques

Dans un circuit fermé constitué de deux conducteurs de nature différente, il circule un courant lorsque l’on maintient entre les deux jonctions une différence de température. Ce phénomène, lié à l’effet Peltier, est utilisé pour la réalisation de sondes thermométriques très précises. La force électromotrice qui apparaît dans le circuit dépend de la nature des deux conducteurs et des températures des deux jonctions: celles-ci sont appelées respectivement soudure chaude et soudure froide. Une des jonctions est en général maintenue à une température de référence (par exemple 0 ⁰C), l’autre servant de capteur.

Le thermocouple le plus précis est constitué de platine et d’un alliage platine + 10 p. 100 de rhodium (couple Le Chatelier ); la sensibilité est de l’ordre de 10 microvolts par degré. D’autres couples métalliques fournissent jusqu’à 70 microvolts par degré, mais les jonctions entre des corps tels que tellure ou bismuth, ainsi que les couples formés de cristaux de germanium dopés n et p , délivrent des forces électromotrices beaucoup plus considérables; ils sont toutefois difficilement manipulables. Le thermocouple le plus réfractaire (utilisable jusqu’à 2 800 ⁰C) est formé de tungstène et d’un alliage de tungstène et de rhénium. Dans le domaine cryogénique, on peut atteindre 1 K (environ) avec certains couples, formés, par exemple, d’alliages or-cobalt (cf. CRYOLOGIE – Cryophysique).

Le tableau 4 donne une liste des principaux thermocouples métalliques d’usage courant.

Méthodes fondées sur la variation de résistance

La résistance électrique d’un métal augmente avec la température, celle d’un semiconducteur décroît. Le termomètre à résistance de platine , très précis si le métal est pur (rapport des résistances à 100 ⁰C et à 0 ⁰C supérieur à 1,391), peut être utilisé depuis 漣 180 ⁰C jusque vers 1 700 ⁰C: le coefficient moyen de variation de résistance est de 39,2 憐 10^-4 K^-1 entre 0 ⁰C et 100 ⁰C. Cet appareil sert d’étalon de base entre l’ébullition de l’oxygène et la solidification de l’antimoine (tabl. 2). D’autres métaux sont quelquefois utilisés pour la mesure des températures, mais plus rarement; c’est le cas du nickel dont le coefficient moyen est 66,3 憐 10^-4 K^-1 entre 0 ⁰C et 100 ⁰C.

Les semiconducteurs ont une résistance beaucoup plus variable avec la température (le coefficient peut atteindre 200 憐 10^-4 K^-1, la résistance suivant une loi de la forme: R = a exp (b /T), où a et b sont des constantes; cette propriété est souvent utilisée pour la régulation des températures, d’où le nom de thermistances donné aux sondes qui sont réalisées sur ce principe. Les thermistances au germanium peuvent être utilisées jusque vers 450 ⁰C, mais il existe des céramiques qui permettent des mesures jusqu’à 1 000 ⁰C. Aux très basses températures (jusqu’au-dessous de 1 K), on se sert de résistances thermométriques en carbone. Les métaux en couches minces (quelques dizaines de nanomètres) fournissent des résistances thermométriques à très court temps de réponse, leurs coefficients de température sont plus faibles que ceux des métaux massifs et peuvent même devenir négatifs en dessous d’une certaine épaisseur.

Parmi les applications des sondes à résistance et des thermocouples métalliques, on peut citer des pyromètres utilisés en aérodynamique et dans les sciences aérospatiales pour la mesure d’écoulements gazeux, souvent portés à haute température (plus de 1 000 ⁰C). Ces appareils comportent un détecteur thermométrique (résistance ou thermocouple), disposé à l’intérieur d’une conduite où l’on établit un débit gazeux rapide. Mais contrairement à ce qui se passe pour les pyromètres pneumatiques (cf. supra , «Méthodes liées à l’équation d’état d’un gaz ou d’un plasma»), où la température est déduite des propriétés mêmes de l’écoulement, le débit gazeux n’a ici pour rôle que d’accélérer les échanges de chaleur avec un capteur solide, destiné à prendre la même température que le gaz.

Bien que la température soit liée à une agitation désordonnée des molécules, il est permis, dans un écoulement gazeux de vitesse u , de considérer comme une température le rapport: u ²/2C^p . Si un gaz à débit et à enthalpie constants ^{[cf. THERMODYNAMIQUE]} possède une vitesse variable, la somme:

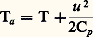demeure fixe (une partie de l’énergie liée aux déplacements désordonnés se transforme en énergie cinétique du mouvement d’ensemble et inversement). T^a est la température d’arrêt, et on appelle u ²/2C^p la température dynamique, la différence T définissant alors la température statique. Des sondes spéciales comportant soit un thermocouple, soit un thermomètre à résistance sont destinées à mesurer la température d’arrêt: le détecteur est disposé dans l’axe d’une conduite où l’on entretient une vitesse suffisante (environ 0,2 fois la vitesse du son) pour assurer un bon échange calorifique avec le gaz: au besoin, cette vitesse est assurée par une aspiration. Dans certaines sondes, on réalise une vitesse sonique sur le capteur thermométrique: celui-ci mesure non plus exactement la température d’arrêt adiabatique, mais une température un peu inférieure (température de frottement) donnée par l’expression:

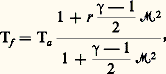où 紐 est le nombre de Mach, 塚 le rapport des chaleurs massiques et r un facteur en général voisin de 0,9; ainsi pour 紐 = 1 et 塚 = 1,4, le rapport des températures absolues T^f /T^a est approximativement égal à 0,98.

Méthodes électriques diverses

On fait encore appel, en thermométrie, pour des applications spéciales à des propriétés électriques diverses telles que la pyroélectricité: celle-ci se manifeste dans certains matériaux piézoélectriques (titanate de baryum), qui prennent une charge électrostatique proportionnelle à l’élévation de température. Les sondes réalisées à partir de ce principe peuvent être utilisées pour des températures peu éloignées de la température ambiante.

Le thermomètre magnétique met en œuvre la susceptibilité de certains corps paramagnétiques, tels que nitrate de cérium et de magnésium, qui varie en fonction inverse de la température (loi de Curie). On peut ainsi effectuer des mesures dans le domaine cryogénique, c’est-à-dire autour de 10^-3 K (cf. CRYOLOGIE – Cryophysique).

Les propriétés électriques des noyaux atomiques sont à la base de procédés intéressants de thermométrie dans le domaine des basses températures. Citons, en particulier, la mesure de la fréquence de résonance quadrupolaire du noyau de chlore dans un cristal de chlorate de potassium; cette résonance, due à l’interaction des champs électriques du réseau avec le moment électrique du noyau, est reliée de façon précise à la température du cristal entre 10 et 100 K.

On citera encore une autre méthode quelquefois utilisée en laboratoire et qui consiste à déduire la température d’une diode au germanium de son courant de saturation: celui-ci est une fonction exponentielle de T jusque vers + 100 ⁰C.

Méthodes thermométriques par variation de luminescence

La fluorescence est une émission lumineuse de certaines substances, qui peut être excitée par un rayonnement de fréquence plus élevée. Cette émission n’est pas d’origine thermique (elle ne suit pas la loi de Planck), mais son intensité varie avec la température. Pour mesurer la température des surfaces solides, on dépose de petites couches de ces substances (anthracène, sulfure de zinc, etc.), que l’on éclaire à l’aide d’une source ultraviolette (fig. 2 a). La lumière émise est analysée et mesurée; on détermine soit la longueur d’onde du maximum d’émission, soit le rapport des intensités de deux raies: la thermosensibilité de ce dernier paramètre peut atteindre 10 p. 100 par degré. Le domaine des températures qui relève de cette méthode s’étend jusque vers 400 ⁰C.

Méthodes optiques et électromagnétiques

La pyrométrie électromagnétique repose sur les lois qui relient la température des corps avec le rayonnement thermique qu’ils émettent ou qu’ils absorbent.

On traitera, en premier lieu, des corps suffisamment denses (solides, liquides ou gaz sous forte épaisseur) dont le rayonnement ne provient que de la surface. La mesure consiste alors à déterminer la température de ce rayonnement: cette température est celle de l’émetteur lui-même si celui-ci est un corps noir; sinon le rayonnement électromagnétique est celui d’un corps noir qui se trouverait à une température plus basse; une mesure exacte exige alors la connaissance du facteur d’émission (cf. MESURE – Mesures optiques).

Les pyromètres dits à radiation totale utilisent le rayonnement émis dans tout le spectre pour échauffer un capteur qui est un élément sensible à la température, tel qu’une résistance thermométrique. À l’aide d’un système optique, le rayonnement est concentré sur ce capteur qui doit l’absorber intégralement; le capteur prend alors, grâce aux pertes de chaleur qu’il subit, une température d’équilibre qui est fonction de l’énergie absorbée, donc de la température à mesurer (bolomètres ).

Le pyromètre monochromatique mesure l’énergie dans un domaine spectral très étroit sélectionné par un filtre (rouge, en général). Un système optique forme l’image de la surface émettrice sur le filament d’une lampe étalon, dont on connaît la température de luminance en fonction du courant de chauffage. Cette température est égale à celle de l’émetteur, quand le filament semble disparaître sur le fond lumineux de l’image. On réalise l’égalité des luminances, soit en déplaçant un coin absorbant (fig. 2 b) qui règle la quantité de lumière admise, la lampe étant alimentée sous tension constante (pyromètre Ribaud ), soit en contrôlant le chauffage du filament.

Les pyromètres à disparition de filament sont utilisables à partir du début de l’incandescence (environ 700 ⁰C) et peuvent être gradués jusqu’à 3 000 ⁰C. Leur utilisation est très courante tant au laboratoire que dans l’industrie, et leur précision peut atteindre deux ou trois degrés.

En pyrométrie optique, la détermination photométrique visuelle peut être remplacée par la photographie; la cinématographie infrarouge permet de suivre l’évolution de températures variables, le film étant étalonné par l’enregistrement de surfaces à températures connues (à partir de 500 ⁰C). Les mesures par cellules photoélectriques sont aussi d’un usage courant; en particulier, la thermovision restitue sur l’écran d’un tube cathodique l’image, en infrarouge lointain, d’une surface émissive, le capteur de rayonnement étant une cellule refroidie; on peut mesurer ainsi avec une grande sensibilité des températures voisines de la température ambiante.

Dans d’autres procédés pyrométriques, les mesures absolues d’énergie font place à des déterminations relatives; la longueur d’onde^m du maximum d’émission est inversement proportionnelle à la température pour un corps noir (cf. formule, in tabl. 2). Le pyromètre à deux couleurs mesure le rapport des intensités émises dans deux raies spectrales, de manière à comparer ce rapport à celui que donne la loi théorique du corps noir; si le facteur d’émission, même inférieur à l’unité, est identique pour les deux longueurs d’onde (corps gris), on atteint directement la température vraie de la surface émettrice.

Le cas des mesures de température de gaz assez épais pour être absorbants mais suffisamment minces pour se laisser traverser par le rayonnement a exigé la mise au point de dispositifs ingénieux, fondés sur le principe d’égalité du facteur d’absorption et du facteur d’émission pour un domaine spectral donné (méthode de renversement des raies spectrales). Son application la plus connue (méthode de Fery) consiste à observer, à l’aide d’un spectroscope, le doublet jaune émis par du sodium pulvérisé dans le gaz; cette raie est superposée à l’émission, dans la même longueur d’onde, d’une lampe étalon à ruban de tungstène située derrière la colonne gazeuse. On règle le chauffage de la lampe de façon que la raie disparaisse sur le fond lumineux: l’énergie émise par le gaz, dans la longueur d’onde considérée, est alors identique à celle qu’il absorbe, provenant de la lampe (fig. 2 c). On démontre que dans ce cas la température vraie du gaz est égale à la température de luminance de la lampe préalablement étalonnée.

Cette méthode peut être rendue automatique en mesurant successivement, à l’aide de cellules photoélectriques, les brillances de la lampe, du gaz et de la lampe vue à travers le gaz; un ordinateur calcule la température à partir de ces trois paramètres; ce dispositif rend possibles des mesures ultrarapides (10^-4 seconde), jusque vers 10⁴ K.

La mesure des températures au sein des milieux gazeux en réaction pose un problème tout particulier, qui a été abordé depuis le début des années 1970 avec des techniques optiques originales et en utilisant l’outil laser. Ces méthodes supplantent rapidement les techniques conventionnelles à sonde mécaniques, car elles ne perturbent ni l’écoulement ni les réactions chimiques. Elles exploitent les propriétés spectrales de diffusion Raman des espèces moléculaires. Historiquement, la première méthode utilisée fut la diffusion Raman spontanée qui s’observe aisément à l’aide d’un laser monochromatique continu ou pulsé de forte puissance. Le faisceau émis par ce laser est focalisé dans le milieu à sonder qui réémet dans toutes les directions un faible rayonnement. Ce dernier contient plusieurs raies, dont une à la fréquence du rayonnement laser excitateur (diffusion de Rayleigh, non utilisée pour les mesures de température) mais aussi deux raies symétriques par rapport à la raie Rayleigh et séparées de cette dernière par la fréquence de vibration des molécules présentes (diffusion Raman). La température est déduite soit du rapport d’intensité des deux raies Raman soit de leur élargissement par la structure rotationnelle; en effet, la fréquence de vibration dépend légèrement de l’état de rotation et les états de rotation ont une population qui est définie par la loi de Boltzmann et change donc avec la température. La diffusion Raman spontanée est relativement bon marché mais peu sensible et difficile à appliquer dans les milieux lumineux.

L’autre méthode, appelée diffusion Raman anti-Stokes cohérente , est née à l’Office national d’études et de recherches aérospatiales (O.N.E.R.A.) et connaît un développement rapide. Elle peut s’observer à l’aide de deux faisceaux laser pulsés intenses et colinéaires focalisés au point à étudier. Si l’écart en fréquence de ces faisceaux est égal à la fréquence de vibration des molécules, un signal lumineux intense est créé dans le milieu. Ce signal apparaît sous la forme d’un faisceau superposé aux deux faisceaux laser excitateurs. Si l’on désigne par 諸¹ et 諸² les fréquences des faisceaux laser, avec 諸¹ 礪 諸², le faisceau signal a pour fréquence 諸¹ + ( 諸¹ 漣 諸²). Sa génération résulte de la diffusion des faisceaux laser incidents par les molécules du gaz, dont la vibration est entraînée de façon synchrone et cohérente par les lasers. Comme le signal apparaît du côté haute fréquence relativement aux faisceaux excitateurs (c’est-à-dire du côté appelé anti-Stokes par les spectroscopistes), et comme il n’est observable que si les modes de vibration des molécules ont une activité Raman, le mécanisme de sa génération a été appelé diffusion Raman anti-Stokes cohérente. La température est déduite de l’élargissement de la raie de vibration par la structure rotationnelle décrite ci-dessus. Cette méthode offre une bonne résolution temporelle (10 ns) et spatiale (1 mm) avec une précision comprise entre quelques K et 100 K sur le domaine de 10 à 4 000 K environ. Elle est applicable aux petits comme aux grands foyers, aux moteurs à pistons comme aux turboréacteurs. Elle rend également de grands services dans l’étude des milieux hors équilibre thermodynamique (plasmas, milieux amplificateurs de lasers, etc.). Ces derniers sont généralement caractérisés par plusieurs températures (de rotation, de vibration, de translation) qui peuvent être mesurées séparément.

Les méthodes électromagnétiques dont il vient d’être question trouvent des applications dans des branches très variées de la science et de la technique. Citons parmi bien d’autres l’astronomie: mesure des températures superficielles des étoiles – le Soleil rayonne à peu près comme un corps noir à 5 900 K – ou des planètes; mesure par l’émission radioélectrique de la température du fond continu du ciel, probablement voisine de 3 K, et qui présente un intérêt fondamental en cosmogonie.

4. Mesure des quantités de chaleur et des flux thermiques

Les mesures calorimétriques se heurtent à une difficulté qui les rend particulièrement délicates, et qui réside dans l’impossibilité d’enfermer ou de canaliser parfaitement la chaleur. Il n’existe pas d’isolant thermique véritable, et un espace, même vide de molécules, est traversé par un rayonnement capable de transmettre un flux thermique.

La calorimétrie

Les calorimètres sont des appareils destinés à mesurer des quantités de chaleur produites ou absorbées par un système. En pratique, on dispose ce système à l’intérieur d’une enceinte calorimétrique. Si, grâce à un isolement thermique, la chaleur demeure emprisonnée dans l’enceinte, aux pertes inévitables près, le calorimètre est dit adiabatique, et la température de l’élément récepteur (avec lequel le système échange sa chaleur) varie au cours de la mesure (calorimètre Berthelot, où la chaleur produite est cédée à une masse d’eau qui s’échauffe). Dans d’autres appareils, l’enceinte calorimétrique cède toute sa chaleur à un milieu extérieur et demeure à température constante: il s’agit d’un calorimètre isotherme, tel que le calorimètre Lavoisier, où la chaleur à mesurer est utilisée pour fondre une certaine masse de glace qui constitue le milieu extérieur.

On ne décrira pas les divers principes des calorimètres (cf. CALORIMÉTRIE ET MICROCALORIMÉTRIE). Signalons seulement que ces appareils ne fournissent qu’une comparaison entre la quantité de chaleur à mesurer et une quantité de chaleur utilisée comme étalon secondaire (par exemple, la chaleur de fusion de la glace dans le calorimètre Lavoisier). De tels étalons secondaires ont dû être définis initialement par comparaison avec l’énergie mécanique, grâce à des expériences fondamentales. Citons, parmi celles-ci, l’expérience de Joule qui permet de déterminer l’équivalent mécanique de la chaleur nécessaire pour échauffer de l’eau (chaleur étalon utilisée dans de nombreux calorimètres adiabatiques). Dans un récipient soigneusement isolé et contenant une masse d’eau connue, on fait tourner un système de palettes entraîné par un moteur, dont le travail peut être mesuré avec précision; ce travail se dissipe sous forme de chaleur dans le liquide grâce à la viscosité, et on détermine ainsi la chaleur massique de l’eau en mesurant son échauffement.

Les fluxmètres thermiques, étalonnage et sources de chaleur

Les fluxmètres thermiques se distinguent des calorimètres en ce sens qu’ils mesurent les dérivées des quantités de chaleur par rapport au temps. Comparés aux fluxmètres, les calorimètres apparaissent ainsi comme des dispositifs intégrateurs.

On mentionnera à part un premier groupe de fluxmètres destinés à la mesure des éclairements énergétiques, grâce à des capteurs spécifiques de rayonnement (photographie, cellules photoélectriques, etc.). Ces appareils mesurent l’énergie thermique rayonnée dans l’unité de temps par la surface de corps chauffés. Dans la mesure où ce flux est une fonction connue de la température de l’émetteur (par exemple, loi du corps noir), les pyromètres optiques sont également des fluxmètres.

Les autres fluxmètres se rangent dans deux catégories: d’une part, les appareils de régime permanent, dont l’élément sensible demeure à une température constante, quand ils sont soumis à un flux constant (ils peuvent être comparés dans une certaine mesure à des calorimètres isothermes, la chaleur absorbée étant à chaque instant compensée par la perte d’une quantité égale); d’autre part, les fluxmètres de régime variable, dont l’élément sensible présente une température fonction du temps quand ils sont soumis à un flux constant. (Ces fluxmètres correspondent aux calorimètres adiabatiques.)

Parmi les appareils fonctionnant en régime permanent, on peut citer: les fluxmètres à circulation de fluide, constitués par une canalisation absorbant le flux thermique à mesurer, et dans laquelle circule un fluide (en général de l’eau) qui s’échauffe; le flux est égal au produit du débit massique, de la chaleur massique et de la différence des températures du fluide à l’entrée et à la sortie de l’appareil. Les fluxmètres à changement d’état sont analogues, pour leur principe, au calorimètre de Lavoisier: le flux est transféré à un corps dont une quantité mesurée subit dans l’unité de temps un changement d’état d’enthalpie massique connue. Les fluxmètres à gradient comportent un détecteur réalisé dans un matériau de conductibilité thermique connue (par exemple, un cylindre dont une extrémité est soumise au flux à mesurer, et l’autre extrémité refroidie à l’aide d’une circulation d’eau). Connaissant la distance qui sépare ces deux extrémités, on calcule le flux absorbé comme le produit de la conductibilité thermique par le gradient de température. L’état d’équilibre entre flux incident à mesurer et flux évacué dans l’appareil, qui caractérise les fluxmètres de régime permanent, peut avoir son origine dans un refroidissement du capteur par rayonnement: un tel capteur est soumis, par exemple, sur une partie de sa surface au flux thermique à mesurer; une autre partie rayonne sur une enceinte à température connue, et perd ainsi, à chaque instant, une quantité de chaleur égale à celle que reçoit le capteur, dès que sa température demeure constante. Connaissant la loi qui relie le flux rayonné à la température (loi du corps noir), la mesure de la température d’équilibre du capteur fournit la valeur du flux absorbé: on retrouve le principe des pyromètres à radiation totale comportant un élément sensible noirci. Les méthodes électriques ont permis aussi de réaliser de nombreux fluxmètres: si le capteur est refroidi par effet Peltier, la chaleur enlevée par unité de temps est égale au flux absorbé dès que la température demeure constante (cette méthode ne s’applique qu’à la mesure de faibles densités de flux, de l’ordre de quelques watts par centimètre carré); si, au contraire, le flux à mesurer tend à refroidir le capteur, par exemple convection dans un écoulement plus froid, on peut le compenser par effet Joule dans une résistance chauffante, qui peut accessoirement servir de thermomètre; on mesure la puissance électrique dissipée quand la température est constante. Ce principe est celui de l’anémomètre à fil chaud, qui permet de déterminer la vitesse d’un écoulement, si l’on connaît la loi qui relie cette vitesse au flux thermique convectif: il comporte un fil très fin (quelques microns) plongé dans le gaz et chauffé par un courant réglable qui entretient une différence de température entre le fil et l’écoulement: le rapport de la puissance électrique dissipée à cette différence de température est égal au coefficient de convection.

Les fluxmètres de régime variable sont d’un emploi plus facile que les précédents et leur précision est généralement meilleure. Les fluxmètres à inertie thermique sont constitués par un élément calorimétrique généralement métallique qui s’échauffe sous l’effet du flux absorbé; on relève la dérivée de la température par rapport au temps, soit d T/dt , et le flux absorbé est fourni par la relation:

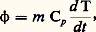où m est la masse de l’élément calorimétrique et C^p sa chaleur massique. Le temps de réponse d’un tel capteur, s’il se présente sous la forme d’un disque d’épaisseur h exposé au flux sur une de ses faces, est de l’ordre de grandeur de h ²/a , a étant la diffusivité thermique. Un métal bon conducteur thermique, de quelques dixièmes de millimètre d’épaisseur, permet de réaliser des fluxmètres dont le temps de réponse n’excède pas quelques millisecondes.

Le fluxmètre à température superficielle permet des mesures avec un temps de réponse encore plus bref: le flux de chaleur est absorbé à la surface d’un capteur formé d’un matériau mauvais conducteur de la chaleur (verre ou silice, par exemple), et suffisamment épais pour que, pendant la durée de la mesure, le signal thermique n’ait pas le temps d’atteindre l’autre face (milieu semi-illimité). La variation de température superficielle suit instantanément le phénomène thermique qui la produit, selon une loi aisément calculable qui fait intervenir le coefficient d’arrachement thermique du matériau. Le temps de réponse d’un tel fluxmètre n’est plus que celui de l’élément thermométrique superficiel, constitué le plus souvent par une résistance métallique en couche mince (quelques centaines d’angströms). Sous cette forme, l’appareil a un temps de réponse inférieur à une centaine de microsecondes, ce qui autorise son emploi pour la mesure de flux très brefs (liés, par exemple, au passage d’une onde de choc). Si l’appareil est soumis à un flux de courte durée et de densité constante 﨏⁰, l’élévation de température superficielle obéit à une équation de la forme:

(cf. supra , chapitre 1, la définition du coefficient d’arrachement thermique).

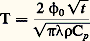L’étalonnage des fluxmètres thermiques exige l’utilisation de sources de chaleur parfaitement reproductibles. Deux possibilités se présentent alors: ou bien on dissipe dans l’appareil à étalonner un flux thermique connu (méthode directe), ou bien on compare cet appareil à un fluxmètre étalon soumis au même flux. La méthode directe est applicable lorsqu’on peut faire passer un courant électrique dans le capteur, qui s’échauffe sous l’effet de la puissance dissipée. La méthode indirecte la plus précise consiste à placer le fluxmètre et l’étalon sous une source de rayonnement; les deux appareils sont noircis (de préférence par du noir de fumée de façon à leur assurer un facteur d’absorption identique). Les fluxmètres étalons sont, soit des capteurs à inertie dont la chaleur massique est parfaitement connue, soit des fluxmètres à circulation d’eau. Les sources de rayonnement peuvent être constituées de tubes incandescents à filament de tungstène. (On obtient ainsi 20 à 30 W/cm² sous tension nominale, et jusqu’à 150 W/cm² pendant des temps brefs en alimentant les tubes sous des tensions plus élevées.) On utilise aussi des fours à image d’arc; un arc électrique de quelques centaines d’ampères est établi entre deux charbons; le cratère positif est disposé au foyer d’un miroir parabolique, et son image est formée au foyer d’un second miroir identique, où l’on dispose les fluxmètres. (Les densités de flux obtenues atteignent 500 W/cm² sur des surfaces de l’ordre du centimètre carré.) Enfin, le bombardement des capteurs par le faisceau d’un canon électronique permet d’obtenir des densités de plusieurs kilowatts par centimètre carré. Signalons que l’utilisation comme source de chaleur de la flamme d’un chalumeau ne permet pas d’obtenir aisément des flux thermiques reproductibles; cette méthode est toutefois utilisée dans certains laboratoires.

Les mesures calorimétriques et celles des flux de chaleur sont d’un usage courant dans l’industrie et au laboratoire. L’étude des divers échangeurs thermiques exige la connaissance des flux transportés: circulation de métaux liquides dans les réacteurs atomiques; échangeurs à ébullition utilisant les transferts de chaleur importants qui se produisent dans un liquide, lors de la transition entre l’ébullition nucléée et l’ébullition par film de vapeur (flux critique maximal). Les techniques spatiales mettent en œuvre des couches thermoprotectrices (matériaux d’ablation) pour dissiper la chaleur engendrée par les engins à grande vitesse traversant l’atmosphère: la décomposition et la sublimation de ces matériaux absorbent de grosses quantités de chaleur qu’il importe de connaître par des mesures préalables. La chimie et la biologie s’intéressent aux chaleurs de réaction. Les techniques de chauffage et de propulsion exigent de nombreuses mesures calorimétriques pour l’étude des processus exothermiques.

5. Mesure des propriétés thermiques

La mesure des conductibilités fait appel à une méthode fluxmétrique. Dans un échantillon de longueur connue d’un matériau déterminé, on crée un gradient thermique permanent en chauffant une extrémité (par exemple, par effet Joule) et en refroidissant l’autre. On détermine, en outre, le flux qui traverse l’échantillon, et la conductibilité thermique est déduite de la valeur de ce flux et du gradient de température, selon l’équation (1). Une telle méthode est particulièrement délicate dans le cas des fluides, la convection naturelle perturbant le transfert de chaleur par conduction. Dans un gaz raréfié, en régime moléculaire, la notion de gradient thermique n’a plus de signification, et les transferts de chaleur par conduction dépendent essentiellement de la pression, alors que la conductibilité d’un gaz dense en est indépendante. La mesure des chaleurs massiques des solides peut être effectuée par un calorimètre, dans lequel on introduit un échantillon préalablement chauffé à une température connue. Lors du refroidissement de l’échantillon, la chaleur cédée au calorimètre est mesurée; connaissant sa masse et sa variation de température, on déduit la chaleur massique moyenne de l’échantillon dans l’intervalle de température utilisé. Une méthode fluxmétrique est également applicable pour des matériaux solides: une masse donnée est soumise à un flux de chaleur connu, et l’on mesure la dérivée, par rapport au temps, de sa température (cf. supra , description du fluxmètre à inertie thermique).

La chaleur massique C^p d’un gaz peut être mesurée en établissant un débit connu sur une résistance chauffante; la connaissance de l’énergie cédée au gaz par effet Joule, du débit et de l’élévation de température du gaz entre l’entrée et la sortie de l’appareil permet le calcul de la chaleur massique.

La diffusivité (/ 福C^p ) peut être calculée à partir de mesures de températures effectuées en différents points d’un matériau soumis à un flux de chaleur. On enregistre l’évolution de ces températures en régime variable et on déduit la diffusivité à partir d’une équation analogue à (3), où l’on remplace le potentiel P par la température T; le coefficient cherché est le rapport de la dérivée:

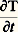à la dérivée seconde:

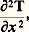si x est la direction normale aux surfaces isothermes. Cette méthode, utilisée pour les isolants, est peu précise en raison de la difficulté qui s’attache à la détermination graphique de la dérivée seconde. Un autre procédé applicable aux conducteurs thermiques est le suivant: un signal thermique sinusoïdal est créé sur la face d’entrée d’un échantillon cylindrique. La mesure de la variation de température, à une distance connue de cette surface, permet de déterminer, soit l’affaiblissement de l’amplitude, soit le déphasage qui sont reliés par une loi simple à la diffusivité.

Le coefficient d’arrachement thermique:

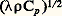est calculé à partir du refroidissement d’un bloc calorimétrique, de capacité calorifique connue, mis en contact aussi parfait que possible avec l’échantillon à essayer (en général, un mauvais conducteur thermique); le coefficient cherché est déduit de l’équation (4): c’est la méthode du touchau .

Le rapport 塚 des chaleurs massiques d’un gaz peut être mesuré à partir de la vitesse du son dans ce gaz, si l’on connaît la masse molaire et la température. Citons encore la méthode de Clement et Desormes: un récipient contenant le gaz à étudier est relié à un manomètre différentiel et comporte un orifice muni d’un robinet; on réalise une variation de pression entre le gaz et l’extérieur, et, après fermeture du robinet, on attend l’équilibre thermique: on lit alors une pression p ¹ sur le manomètre. On ouvre le robinet jusqu’à équilibre des pressions, puis on le referme. Après le retour du gaz à la température ambiante, une nouvelle différence de pression p ² apparaît; on démontre que 塚 est égal au rapport: p ¹/(p ¹ 漣 p ²).

Encyclopédie Universelle. 2012.